Mecanismes

Mecanismes#

Pàgina en desenvolupament

Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.

En aquest vídeo podeu veure alguns mecanismes en acció:

Mecanismes de transmissió del moviment#

No es canvia lel tipus de moviment, però s’aconsegueix un canvi en la direcció, sentit o velocitat.

Relació de transmissió#

La relació de transmissió \(\tau\) indica el nombre de voltes que fa l’eix conduït (sortida) per cada volta de l’eix motriu (entrada). Dividint pel temps:

\(\tau = \frac {\omega_2}{\omega_1}\)

on \(\omega_1\) és la velocitat angular de l’eix motriu i \(\omega_2\) la de l’eix conduït.

Típicament aquesta ràtio és inversa a la mida dels components: quan més grans, més lents van. Això s’aplica a engranatges, transmissió de cadena (per exemple a una bicicleta), discs de fricció …

Cardan#

Només canvia la direcció de l’eix de gir.

\(\tau = 1\)

By Van helsing - Treball propi, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1499089

Engranatges#

S’inverteix el sentit de gir

\(\tau = \frac{z_1}{z_2}\)

on \(z_1\) és el nombre de dents de l’engranatge motriu i \(z_2\) el nombre de dents de l’engranatge conduït.

Es defineix el diàmetre primitiu com

\(D_p \equiv \frac{p \cdot z}{\pi}\)

i es defineix el mòdul com

\(M \equiv \frac{D_p}{z} = \frac{p}{\pi}\)

Dos engranatges amb el mateix mòdul engranaran sense problemes.

Si volem canviar la direcció de l’eix de gir 90° podem utilitzar engranatges cònics.

Càlcul del Moment#

\(P_2 = \eta \cdot P_1\)

\(\Gamma_2 \cdot \omega_2= \eta \cdot \Gamma_1 \cdot \omega_1\)

\(\Gamma_2 = \eta \cdot \Gamma_1 \cdot \frac{\omega_1}{\omega_2}\)

\(\Gamma_2 = \frac{\eta}{\tau} \cdot \Gamma_1\)

Trens d’engranatges#

\(\tau \equiv \frac{\omega_n}{\omega_1} = \frac{\omega_n}{\omega_{n-1}}\frac{\omega_{n-1}}{\omega_{n-2}}\cdot\cdot\cdot\frac{\omega_3}{\omega_2}\frac{\omega_2}{\omega_1}\)

Cal tenir present que \(\frac{\omega_i}{\omega_{i-1}} = 1\) si els dos engranatges són solidaris

Exemple

\(z_1=14\) (vermell); \(z_2=42\) (blau); \(z_3=14\) (groc); \(z_4=28\) (verd).

\(\tau \equiv \frac{\omega_4}{\omega_1} = \frac{\omega_4}{\omega_{3}}\frac{\omega_{3}}{\omega_{2}}\frac{\omega_2}{\omega_1} = \frac{14}{28} \cdot 1 \cdot \frac{14}{42} = \frac{196}{1176} \cong 0,17\)

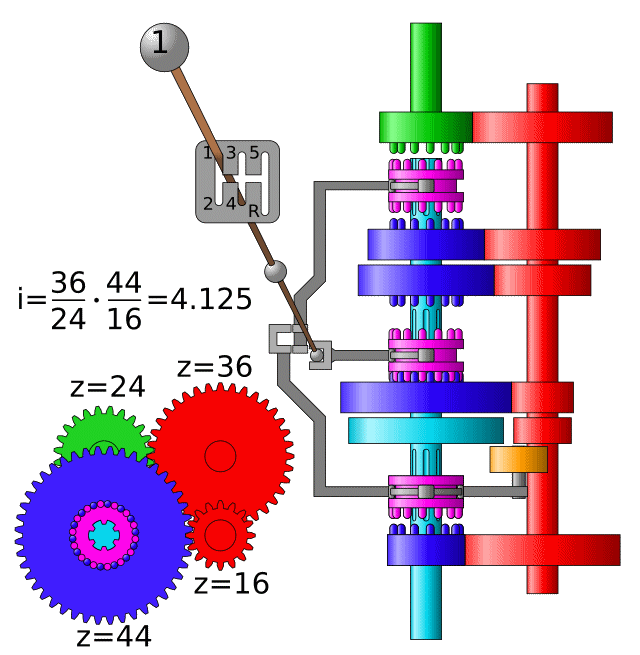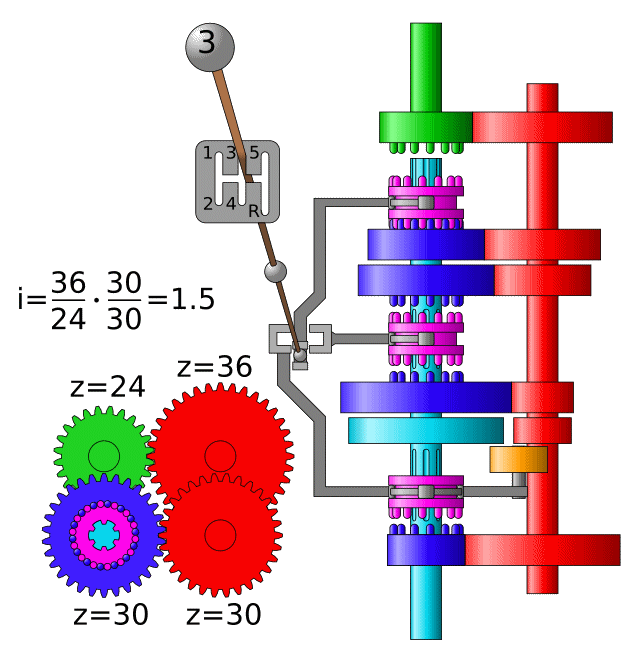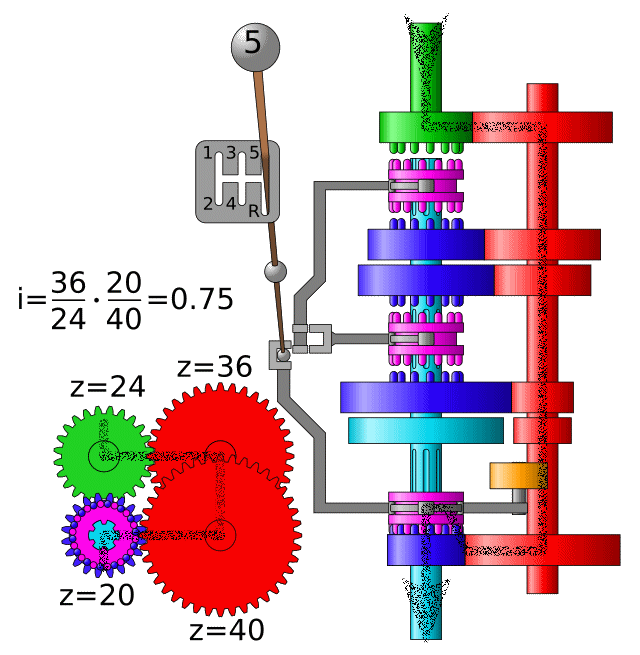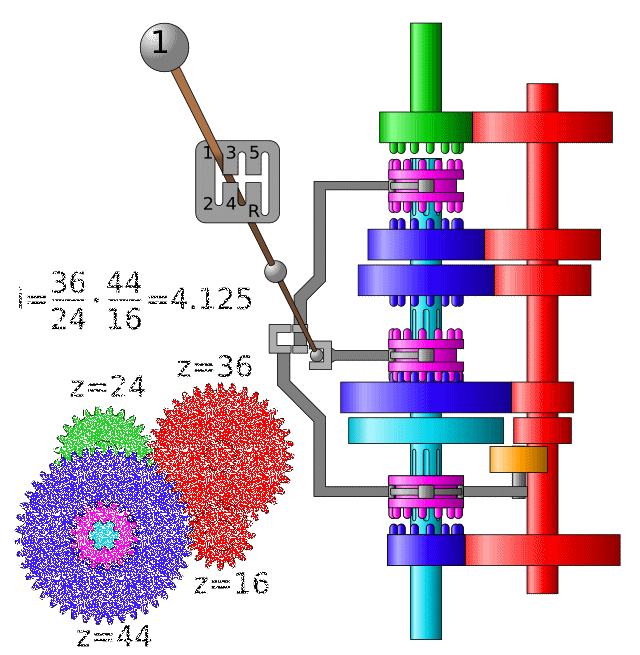
Aplicació: Caixa de canvis#

Compte! El valor mostrat a l’animació és \(i = \frac{1}{\tau}\)

Cargol sense fi#

\(n_1 \cdot e_1 = n_2 \cdot Z_2\)

on \(n_i\) són les velocitats angulars, \(Z_2\) el nombre de dents de la roda conduida i \(e_1\) el nombre d’helix del cargol.

Per tant, la relació de transmissió val

\(\tau = \frac{e_1}{Z_2}\)

Es tracta d’un mecanisme reductor molt potent

Engranatges planetaris#

Són sistemes molt compactes, flexibles i més complexos. Segons bloquegem l’engranatge central (planetari), l’engranatge més extern (anular o corona) o els satèlits intermitjos canvia el seu comportament:

Mecanisme diferencial#

Justament basat en el bloqueig dels engranatges planetaris, permet que les rodes del cotxe girin a diferent velocitat quan agafem una corba.

Mecanismes de transformació del moviment#

El tipus de moviment generat no es el mateix que el motriu

Cargol / femella#

Transforma un moviment circular en linial. Molt utilitzat en impressores 3D i d’altres màquines de precissió.

Si fem una volta la femella avança el pas p

\(v = \omega \cdot \frac{p}{2\pi}\)

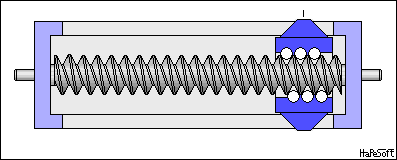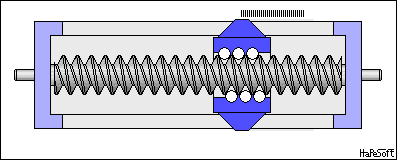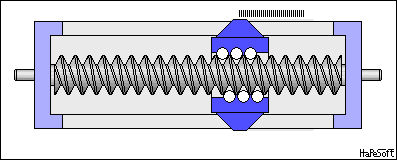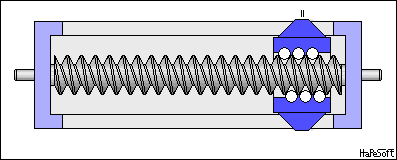
By W.Rebel - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=7931115

Pinyó / cremallera#

Com en una volta el pinyó avança \(z\) dents amb pas \(p\)

\(v = z \cdot p \cdot \frac{\omega}{2\pi}\)

Lleva i excèntrica#

Biela / manovella#

Transforma el moviment alternatiu en circular i viceversa. Utilitzat als motors de combustió interna i moltes altres màquines.

Creu de malta#

Encara que el moviment conduït també és circular, és de caràcter intermitent. Utilitzat en projectors de cinema, cintes de transport a fàbriques automàtiques, armes a avions d’hèlix …

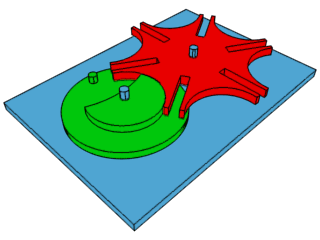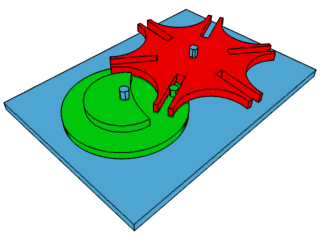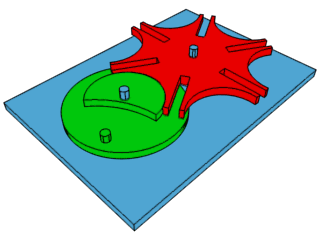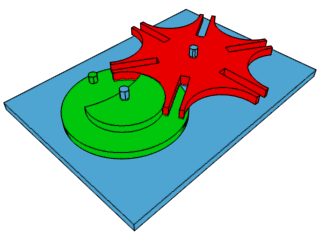
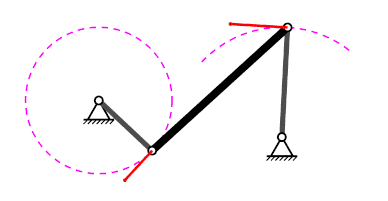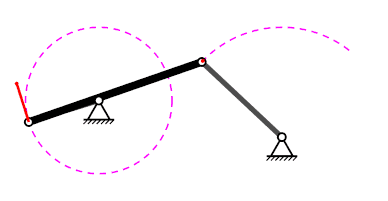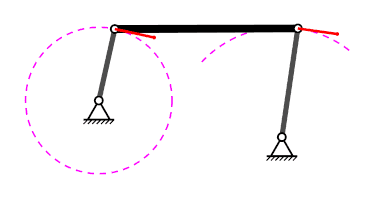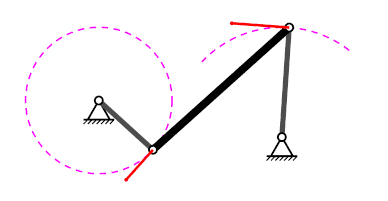
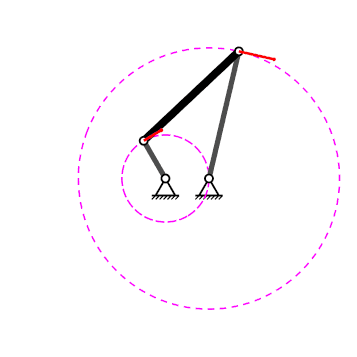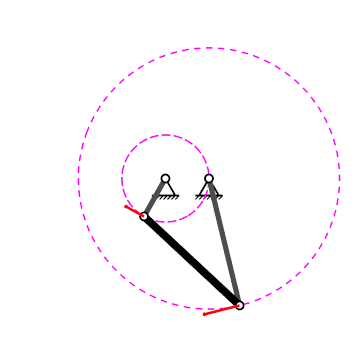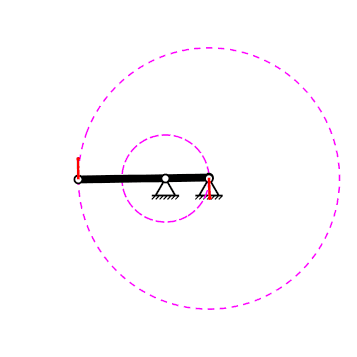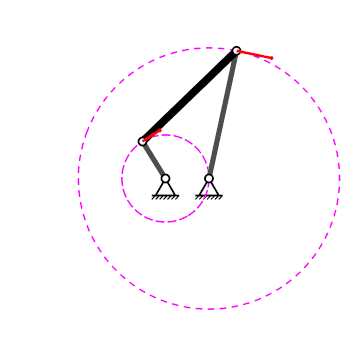
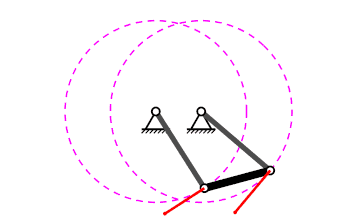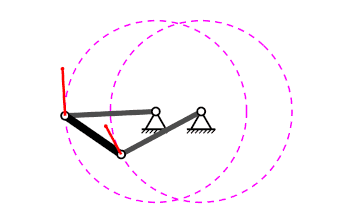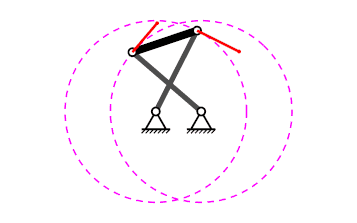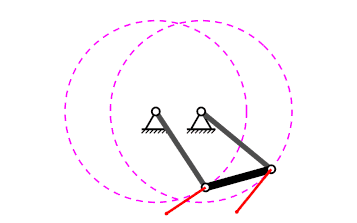
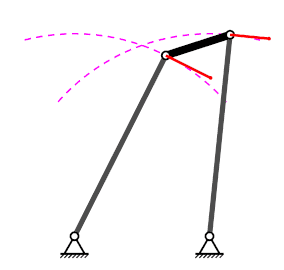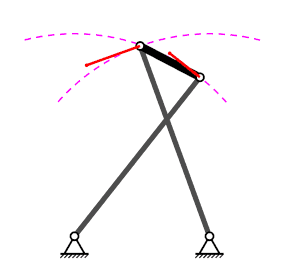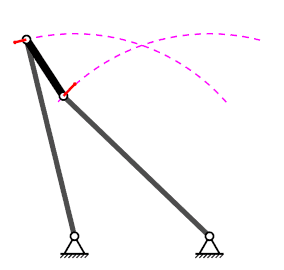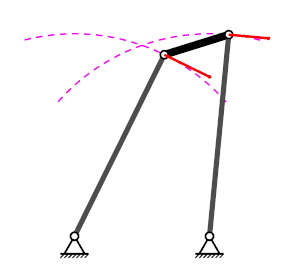
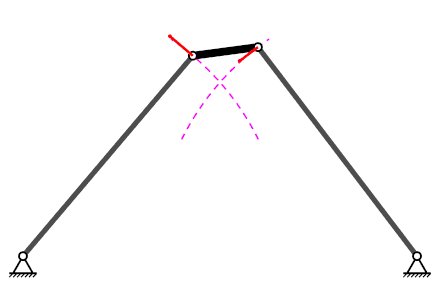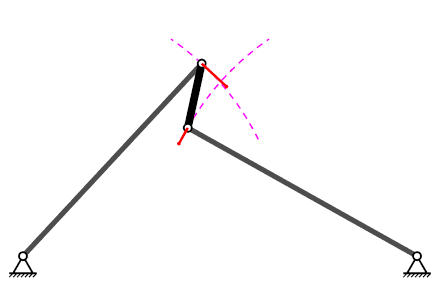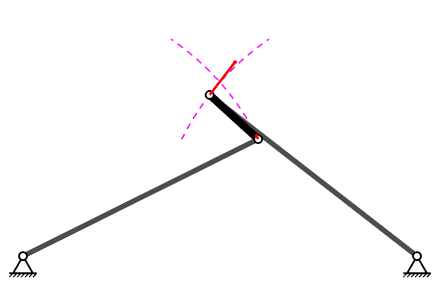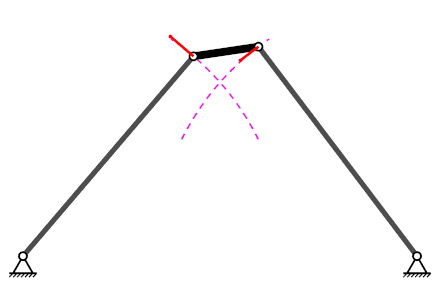
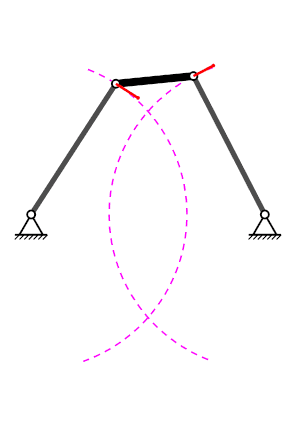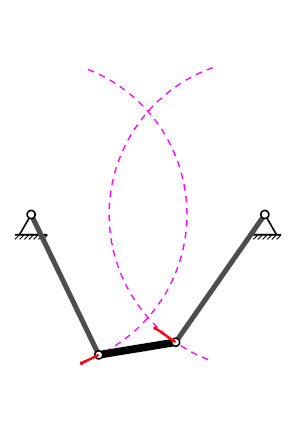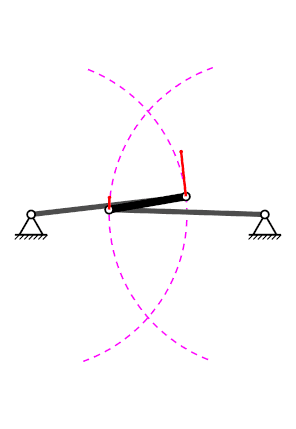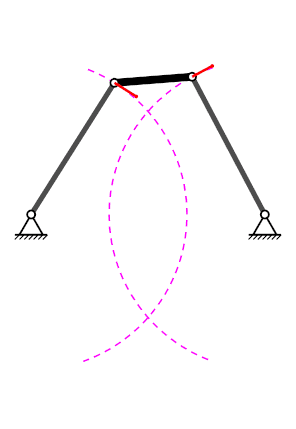
Mecanisme de quatre baules#