Exercicis resolts 2/2

PAU 2005 S1 4B

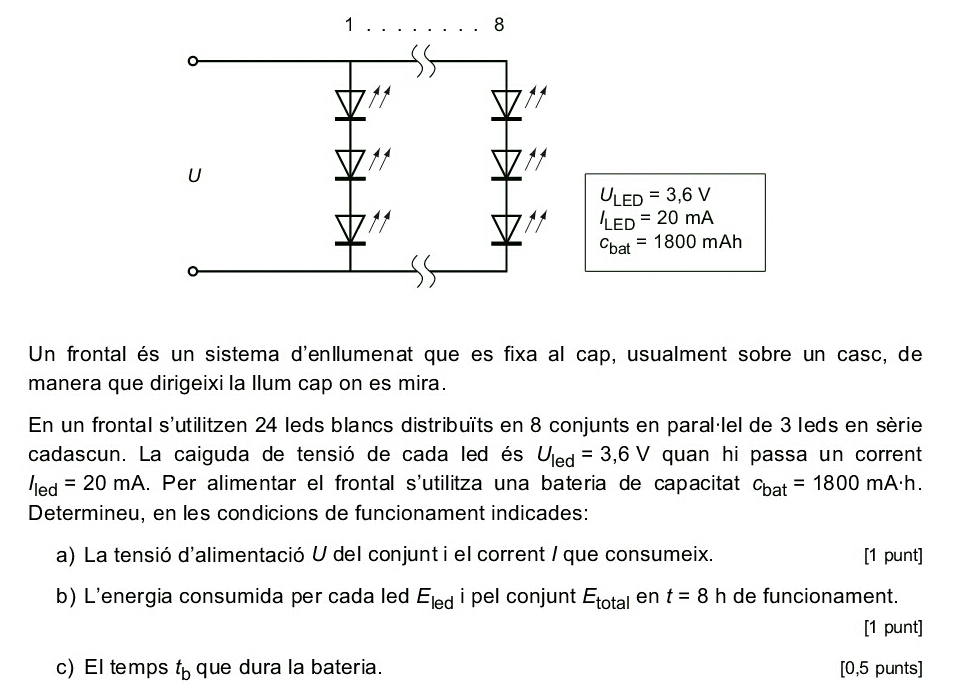
a)

\(U = 3 \cdot U_{led}\)

\(I = 8 \cdot I_{led}\)

U = 3*3.6
I = 8*20E-3
U,I

(10.8, 0.16)

\(E_{led} = U_{led} \cdot I_{led} \cdot t\)

\(E_{total} = 24 \cdot E_{led}\)

Eled=3.6*20E-3*8
Etotal=24*Eled
Eled,Etotal

(0.5760000000000001, 13.824000000000002)

\(\Large t_b=\frac{c_{bat}}{I}\)

tb=1.8/I
tb

11.25

PAU 2009 S4 4B

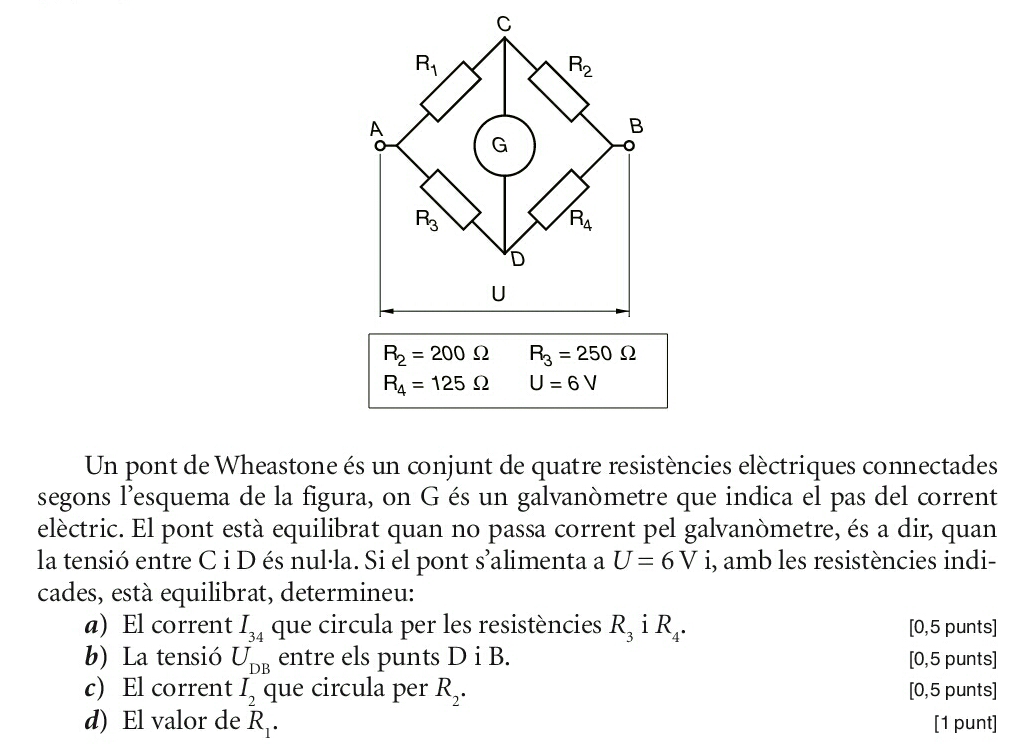
a)

\(\Large U = I_{34} \cdot (R_3 + R_4) \Rightarrow I_{34} = \frac{U}{R_3+R_4}\)

I34=6/(250+125)
I34

0.016

b)

\( U_{DB} = I_{34} \cdot R_4 \)

Udb=I34*125
Udb

2.0

c)

pont equil·librat \(\Rightarrow U_{CB} = U_{DB}\)

\(\Large I_2 = \frac{U_{CB}}{R_2} = \frac{U_{DB}}{R_2}\)

I2=Udb/200
I2

0.01

d)

pont equil·librat \(\Rightarrow I_1 = I_2\)

\(U = I_1 \cdot R_1 + I_2 \cdot R_2 = I_2 \cdot (R_1+R_2)\)

\(\Large \Rightarrow R_1 = \frac{U}{I_2} - R_2 \)

R1=6/I2-200
R1

400.0

Per entendre millor aquest problema et recomano aquesta animació. Al nostre problema \(R_1\) és el valor desconegut i \(R_2\) el valor ajustat amb una caixa de resistències.