Pràctica: Estudi d’una pila i d’una bombeta#
Objectius#
Aprendre el funcionament del polímetre com a voltímetre, amperímetre i ohmímetre
Fer una estimació de la força elecromotriu (\( \varepsilon \)) i de la resistència interna (\(r\)) d’una pila$
Observar com cau el voltatge d’una pila quan subministra potència a una càrrega
Observar com la resistència d’una bombeta varia amb la temperatura i fer una estimació de la temperatura de funcionament
Materials#
Polímetre
Pila de petaca
Bombeta 3,5 V
Cables de connexió
Observació#
Característiques de la bombeta:
Voltatge: 3,8 V
Intensitat: 0,3 A
Característiques de la pila:
Voltatge.: 4,5 V
Mesures prèvies#
Mesura de la resistència de la bombeta amb el polímetre configrat com a ohmímetre:
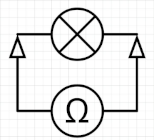
Resistència (\(R_0\)): \(1,7 \Omega\)
Mesura de la força electromotriu de la pila amb el polímetre configurat com a voltímetre:
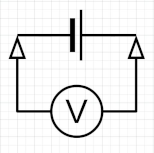
Força electromotriu (\(\varepsilon \)): \(4,2 \Omega \)
Mesures amb el circuit connectat#
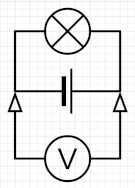
Voltatge (U): 3,6 V
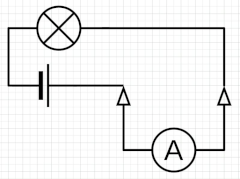
Intensitat (I): 0,25 A
Càlculs#
Calculem la resistència de la bombeta encesa:
\(\Large R_T = \frac{U}{I} = \frac{3,6 V}{0,25 A} = 14,4 \Omega\)
Calculem la resistència interna de la pila:
\(\Large r = \frac{\varepsilon - U}{I} = \frac{4,2 V - 3,6 V}{0,25 A} = 3,6 \Omega\)
Estimem la temperatura del filament:
\(\rho_t = \rho_{20} \cdot [1 + \alpha \cdot (t-20 ^{\circ} C)]\)
La mateixa relació tenim entre les resistències, ja que ni L ni s varien de forma significativa. Suposant que el taller està a \(20 ^{\circ} C\):
\(\Large \frac{R_T}{R_0} = 1 + \alpha (t - 20 ^{\circ} C)\)
Per al tungsté \(\alpha = 0,0045\)
Amb aquestes dades, podem fer una estimació de la temperatura del fil de tungsté:
\(\Large t = \frac{\frac{14,4}{1,7}-1}{0,0045} + 20 ^{\circ} C \simeq 1680 ^{\circ} C\)