La potència a AC#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
Al corrent altern hem de parlar de potències, en plural:
Potència aparent#
\(S \equiv U \cdot \overline{I}\)
S és la potència aparent, i es mesera en volt ampers (VA). No és una potència útil, ja que contempla la component imaginària Q que s’emmagatzema en bobines i condensadors en forma de camps magnètics i electrics.
Potència activa#
\(P \equiv U \cdot I \ cos\varphi\)
Aquesta és la potencia real, que es mesura en watts (W). Aquí si que l’energia elèctrica es transforma en treball útil o calor. Justament per aixó \(cos\varphi\) s’anomena factor de potència
\( P = I^2 \ R \)
Potència reactiva#
\(Q \equiv U \cdot I \ sin\varphi\)
Es mesura en volt ampers reactius (var). És la component imàginaria de S que abans comentavem, no produeix treball. Els fluxos d’energia s’emmagatzemen en bobines i condensadors en forma de camps magnètics i electrics quan engeguem el circuit i es tornen quan el desconectem, apareixent com a efectes transitoris d’encesa/apagada del circuit.
\( Q_C = I^2 \ X_C \)
\( Q_L = I^2 \ X_L \)
\( Q = I^2 \ (X_L - X_C) \)
Continuem amb l’exemple anterior del circuit amb una resistència i un condensador que vam utilitzar al tema d’impedàncies:
import numpy as np
import matplotlib.pyplot as plt
R = 10
C = 162.48 * 10**(-6)
U = 220
f = 50
w = 2 * np.pi * f
Xc = 0 -1j/(C*w)
Z = R + Xc
I = U/Z
S = U * np.conj(I)
modS = np.abs(S)
modS
2200.463803676809
angS = np.degrees(np.angle(S))
angS
-62.958143957668284
\(S = 2200_{-62,96^{\circ}} \ VA\)
P = np.real(S)
P
1000.4216841512007
\(P = 1000 \ W\)
angZ = np.degrees(np.angle(Z))
fdp = np.cos(angZ)
fdp
0.9920358997298501
\(cos(\varphi) = 0,9920\)
Q = np.imag(S)
Q
-1959.8972945468051
\(Q = -1960 \ var\)
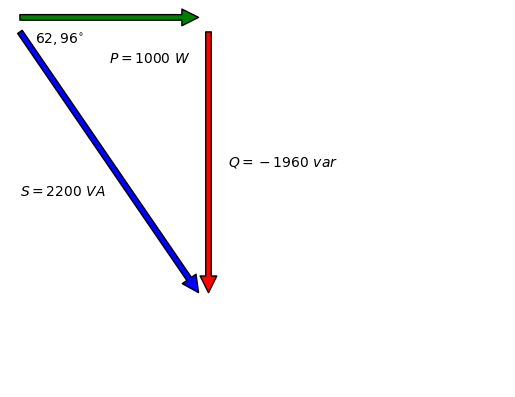
Triangle de potències#
Com a la fòrmula la I va conjugada, el triangle de potències és un trangle matemàticament semblant al d’impedàncies.
Representem les potències i visualitzem el riangle de potències
Show code cell source
%matplotlib inline
plt.annotate('', xy=(np.real(S), np.imag(S)), xytext=(0, 0),
arrowprops=dict(facecolor='blue', shrink=0.05),
)
plt.annotate('', xy=(np.real(S), 0), xytext=(0, 0),
arrowprops=dict(facecolor='green', shrink=0.05),
)
plt.annotate('', xy=(np.real(S), np.imag(S)), xytext=(np.real(S), 0),
arrowprops=dict(facecolor='red', shrink=0.05),
)
plt.annotate("$S = 2200 \ VA$", xy=(50, -1200))
plt.annotate("$P = 1000 \ W$", xy=(500, -300))
plt.annotate("$Q = -1960 \ var$", xy=(1100,-1000))
plt.annotate("$62,96^{\circ}$", xy=(125,-175))
plt.xlim(0, 2500)
plt.ylim(-2500, 0)
plt.axis('off')
plt.show()