Àlgebra de Boole#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
Una mica d’Història#
Tots coneixeu el sistemes digitals; només poden agafar dos valor: 0 o 1. El que potser no conegueu és que aquests sistemes es poden analitzar i dissenyar amb una estructura matemàtica publicada per George Boole al 1847, coneguda com a àlgebra de Boole. No només l’electrònica digital se n’aprofita. La lògica proposicional, els diagrames de Venn, l’enginyeria pneumàtica, la programació informàtica, el disseny 3D, l’electricitat industrial i moltes més disciplines també l’utilitzen [con23a]. De fet, Claude Shannon (si, el mateix que va introduir el concepte d’entropia de la informació) va ser dels primers en utilitzar-la; la va fer servir per analitzar els circuits amb relés i conmutadors, tema de la seva tesis doctoral del 1937 [con24].
Com té aplicació a moltes disciplines cadascuna ha adaptat la simbologia al seu camp. Per ara utilitzarem la simbologia de l’electrònica digital. Al final del tema trobareu l’equivalència amb altres disiplines.
Definició#
\(\mathcal{B}=\left\{0.1\right\}\)
\((+ \ , \ \cdot) \ \) operacions
L’estructura \((\mathfrak{B}, +, \cdot)\) és un àlgebra de Boole quan es cumpleixen els 5 postulats de Huntington
Postulats de Huntington#
\(\forall \ a,b,c\in \mathcal{B}\)
Primer postulat: les operacions són internes:
\(a+b\in \mathcal{B}\qquad a\cdot b\in \mathcal{B} \qquad\)
Segon postulat: existeix un element neutre per a cada operació:
\(a+0 = a\qquad a\cdot 1 = a \qquad\)
Tercer postulat: existeix l’element invers:
\(a\cdot \overline{a} = 0\qquad a+\overline{a} = 1 \qquad\)
Quart postulat: existeix la propietat commutativa:
\(a+b = b+a\qquad a\cdot b = b\cdot a \qquad\)
Cinquè postulat: existeix la propietat distributiva:
\(a\cdot (b+c) = (a\cdot b)+(a\cdot c)\qquad a+(b\cdot c) = (a+b)\cdot (a+c) \qquad\)
Altres propietats#
Lleis d’absorció:
\(a+(a\cdot b) = a\qquad a\cdot (a+b) = a\qquad\)
\(a+(\overline{a}\cdot b) = a+b\qquad a\cdot (\overline{a}+b) = a\cdot b\qquad\)
Llei d’idempotència:
\(a+a=a\quad a\cdot a= a\qquad\)
Llei d’involució:
\(\overline{(\overline{a})} = a\qquad\)
Llei de De Morgan:
\(\overline{a+b} = \overline{a}\cdot\overline{b}\qquad \overline{a\cdot b} = \overline{a}+\overline{b}\qquad\)
Propietat associativa:
\(a+(b+c)=(a+b)+c\qquad a\cdot(b\cdot c)=(a\cdot b)\cdot c\qquad\)
Simbologia a altres disciplines#
Disciplina |
Operació 1 |
Operació 2 |
Element neutre operació 1 |
Element neutre operació 2 |
Element |
Invers |
|---|---|---|---|---|---|---|
Electrònica digital |
+ |
\(\cdot\) |
0 |
1 |
a |
\(\overline{a}\) |
Lógica proposicional |
o |
i |
F |
V |
p |
¬p |
Àlgebra de Venn |
\(\cup\) |
\(\cap\) |
\(\emptyset\) |
U |
A |
\(A^\complement\) |
Portes lógiques |
OR |
AND |
L |
H |
A |
NOT A |
Llenguatge C |
|| |
&& |
false |
true |
nomVariable |
!nomVariable |
Llenguatge Python |
or |
and |
False |
True |
nomVariable |
not nomVariable |
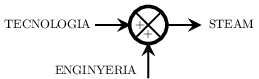
Simbología gràfica#
Portes lògiques ISO#
OR |
AND |
NOT |
NOR |
NAND |
XOR |
|---|---|---|---|---|---|
Portes lògiques ANSI#
OR |
AND |
NOT |
NOR |
NAND |
XOR |
|---|---|---|---|---|---|
Taules de veritat#
Porta OR#
a |
b |
a + b |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Porta AND#
a |
b |
a \(\cdot\) b |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Porta NOT#
a |
\(\overline{a}\) |
|---|---|
0 |
1 |
1 |
0 |
Funcions lògiques combinacionals#
Qualsevol expressió en l’algebra de Boole és una funció lògica. La lògica combinacional es limita a expressions que només depenen de l’entrada actual. A la lògica seqüencial la sortida no només depèn de l’entrada actual, sinó també de la història de l’entrada.
Truc
Equivalència de funcions lògiques: dues funcions lògiques són equivalents si comparteixen la mateixa taula de veritat
Podem comprovar la validesa de les lleis de De Morgan comparant les seves taules de veritat
a |
b |
NOT (a OR b) |
NOT a |
NOT b |
(NOT a) AND (NOT b) |
|---|---|---|---|---|---|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Al llarg d’aquest capítol faré servir el següent exemple de funció lògica, del qual, per ara, desconeixem la seva expressió algebraica:
a |
b |
c |
d |
s |
|
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
1 |
0 |
4 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
6 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
8 |
1 |
0 |
0 |
0 |
1 |
9 |
1 |
0 |
0 |
1 |
1 |
10 |
1 |
0 |
1 |
0 |
1 |
11 |
1 |
0 |
1 |
1 |
0 |
12 |
1 |
1 |
0 |
0 |
1 |
13 |
1 |
1 |
0 |
1 |
0 |
14 |
1 |
1 |
1 |
0 |
1 |
15 |
1 |
1 |
1 |
1 |
0 |
minterms#
Podem expresar la nostra funció lògica com a una suma amb productes de minterms. Cada minterm és un producte de les variables d’entrada , negades si el seu valor es 0; o dit d’una altra manera, el producte de la representació binària del seu índex. Només els minterms on la sortida és 1 apareixen a l’expressió.
Veiem l’expressió amb mintems de la nostra funció exemple:
\(s = m_0 + m_1 + m_2 + m_8 + m_9 + m_{10} + m_{12} + m_{14}\)
\(s = \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot d + \overline{a} \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d}+ a \cdot \overline{b} \cdot \overline{c} \cdot d + a \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot b \cdot \overline{c} \cdot \overline{d} + a \cdot b \cdot c \cdot \overline{d}\)
Maxterm#
Podem expresar la nostra funció lògica com a un producte de sumes amb maxterms. Cada maxterm és una suma de les variables d’entrada , negades si el seu valor es 1; o dit d’una altra manera, la suma producte dels complementaris de la seva representació binària del seu índex. Només els maxterms on la sortida és 0 apareixen a l’expressió.
\(s = M_3 \cdot M_4 \cdot M_5 \cdot M_6 \cdot M_7 \cdot M_{11} \cdot M_{13} \cdot M_{15}\) \(s = (a+b+\overline{c}+\overline{d}) (a+\overline{b}+c+d) (a+\overline{b}+c+\overline{d}) (a+\overline{b}+\overline{c}+\overline{d}) (a+\overline{b}+\overline{c}+\overline{d}) (\overline{a}+b+\overline{c}+\overline{d}) (\overline{a}+\overline{b}+c+\overline{d}) (\overline{a}+\overline{b}+\overline{c}+\overline{d})\)
Simplificació de funcions lògiques#
Simplificació algebraica#
Es tracta de manipular algebraicament l’expressió de la funció per a obtenir la versió més senzilla possible. Moltes vegades no és gens fàcil. Però existeixen metòdes gràfics, com ara els mapes de Karnaugh o els diagrames de Veitch que ens poden guiar.
Diagrames de Veitch#
Es tracta d’un mètode gràfic on representem totes les combinacions possibles de la taula de veritat. És molt semblant a un altre mètode anomenat mapa de Karnaugh, però el diagrama de Veitch és molt més fàcil interpretar el resultat.
Per a 3 variables:
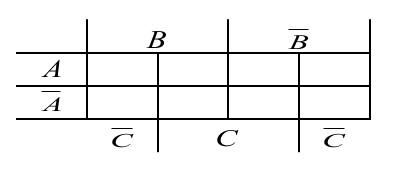
Per a 4 variables:
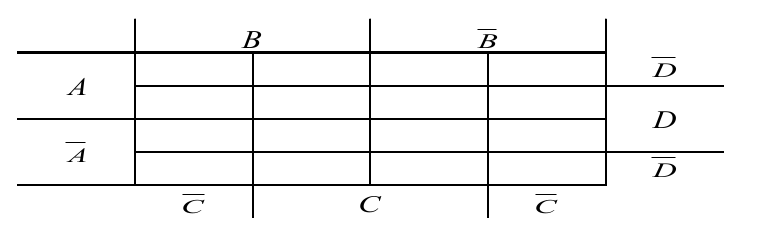
Cal tenir en compte que el costat de l’esquerra enllaça amb el costat de la dreta i que el costat superior enllaça amb el costat inferior, com passa a molts videojocs. En realitat estem treballant sobre una superfície toroidal:

Podeu baixar aquesta plantilla amd diagrames de Veitch per a 2, 3, 4, 5 i 6 variables.
El diagrama s’utilitza així:
Col·loquem els minterms de la nostra funció al diagrama
Busquem grups rectangulars (quadrats inclosos) amb un nombre de termes potència de 2: 1, 2, 4, 8, 16 … Agafem el mínim nombre de grups, els grups més grans possibles, encara que solapin, i que cubreixin tots els nostres minterms.
Interpretem els grups: si la variable té només un valor, és un factor del producte; si presenta els dos valors 0 i 1 no apareix al producte.
Veiem un exemple amb la nostra funció:
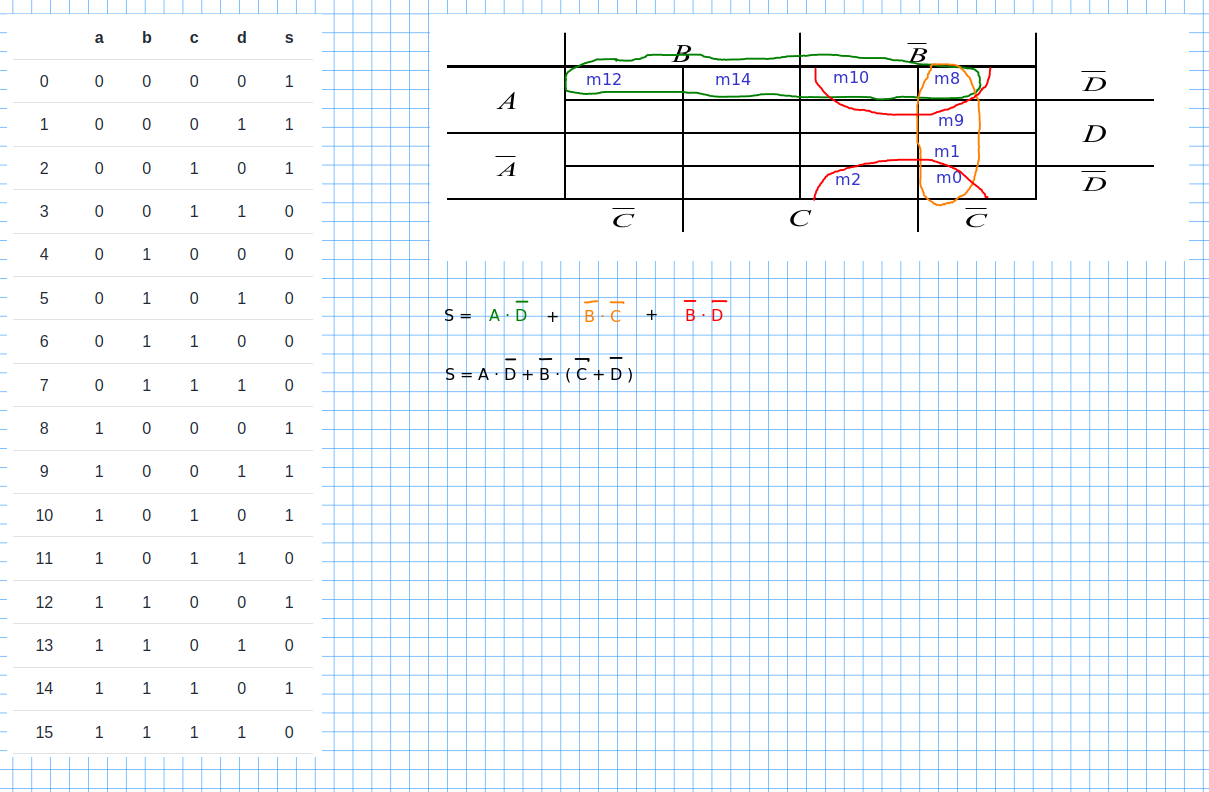
Per tant:
\(s = a \ \overline{d} + \overline{b} \ (\ \overline{c} + \overline{d} \ )\)
En el nostre càs he pogut treure manualment un factor comú \(\overline{b}\) a dos dels termes
Diagrames de Veitch com a guia per a una simplificació algebraica rigurosa#
Podem agafar els grups que hem detectat al diagrama de Veitch. Si a un minterm solapen diversos grups podem repetir el minterm tante vegades com solapi el minterm, gràcies a la propietat d’idempotència:
\(s = \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot d + \overline{a} \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d}+ a \cdot \overline{b} \cdot \overline{c} \cdot d + a \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot d + a \cdot b \cdot c \cdot \overline{d}\)
\(s = \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot d + \overline{a} \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d}+ a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} \ +\)
\(\ \ \ \ \ + \ a \cdot \overline{b} \cdot \overline{c} \cdot d + a \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot b \cdot \overline{c} \cdot \overline{d} + a \cdot b \cdot c \cdot \overline{d}\)
Ara amb les propietats conmutativa i associativa agrupem els termes com als grups que hem obtingut al diagrama de Veitch:
\(s = \left\lfloor \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} +a \cdot \overline{b} \cdot c \cdot \overline{d} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot d + a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{c} \cdot d \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor a \cdot \overline{b} \cdot \overline{c} \cdot \overline{d} + a \cdot \overline{b} \cdot c \cdot \overline{d} + a \cdot b \cdot \overline{c} \cdot \overline{d} + a \cdot b \cdot c \cdot \overline{d} \right\rfloor\)
Ara amb la propieta associativa treiem factors comuns dintre de cada grup:
\(s = \left\lfloor \overline{a} \cdot \overline{b} \cdot (\overline{c} + c) \cdot \overline{d} + a \cdot \overline{b} \cdot (\overline{c} + c) \cdot \overline{d} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot (\overline{d} + d) + a \cdot \overline{b} \cdot \overline{c} \cdot (\overline{d} + d) \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor a \cdot \overline{b} \cdot (\overline{c}+c) \cdot \overline{d} + a \cdot b \cdot ( \overline{c}+c) \cdot \overline{d} \right\rfloor\)
Apliquem que la suma d’inversors és 1 i que 1 és l’element neutre del producte:
\(s = \left\lfloor \overline{a} \cdot \overline{b} \cdot \overline{d} + a \cdot \overline{b} \cdot \overline{d} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor \overline{a} \cdot \overline{b} \cdot \overline{c} + a \cdot \overline{b} \cdot \overline{c} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor a \cdot \overline{b} \cdot \overline{d} + a \cdot b \cdot \overline{d} \right\rfloor\)
Tornem a treure factors comuns:
\(s = \left\lfloor (\overline{a} + a) \cdot \overline{b} \cdot \overline{d} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor (\overline{a} + a) \cdot \overline{b} \cdot \overline{c} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor a \cdot (\overline{b}+b) \cdot \overline{d} \right\rfloor\)
I tornem a aplicar que la suma d’inversors és 1 i que 1 és l’element neutre del producte:
\(s = \left\lfloor \overline{b} \cdot \overline{d} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor \overline{b} \cdot \overline{c} \right\rfloor \ +\)
\(\ \ \ \ \ + \ \left\lfloor a \cdot \overline{d} \right\rfloor\)
Programari de simplificació#
Utilitzar programari és molt còmode. En aquest que us mostro heu d’escollir l’opció SOP (suma de productes) per obtenir el minterm
Show code cell source
%%html
<iframe src="http://www.32x8.com/index.html" width="800" height="800"></iframe>
Obrir el programari a una altra finestra del navegador
Utilitzem aquest programari amb la nostra funció exemple:
Show code cell source
%%html
<iframe src="http://www.32x8.com/sop4_____A-B-C-D_____m_0-1-2-8-9-10-12-14___________option-8_____898788975272827595797" width="800" height="800"></iframe>
Si us fixeu bé, la diferent ordenació de les variables al mapa en aquest programari ha situat el grup \(\overline{b} \cdot \overline{d}\) a les quatre posicions de les cantonades, que també formen un quadrat a l’espai toroidal
Esquema de portes lògiques#
Simulació amb programari#
Per visualitzar els símbols en format ISO cal anar a Options -> IEC Gates
Show code cell source
%%html
<iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcMBMcUHYMGZIA4UA2ATmIxAUgoqoQFMBaMMAKABlwwVxCqAWPDyrCQAMwCGAGwDOdapHaduaQQJAqomiTLlIFHZsoSEQalMc1Vts+SwCSSoeGLcwvS9CQJ7jjWBfq+B5ePobqFv5GJsKeFCxglOp4glyC2Hh84CiCVNy08YnZghrpmRq51N4JuclJaRl1mtwhAO7Oru4oKJluwixtXT2d3e1Q-eojkY1TCm1TfgGDY3OLI0UTmbMbo0uYeeO7GMq1e8s7EQG4mwcWV413W+tgfGURL2fmJs+vJg-jU3dPiA-gluHxsMoggguIEcsDKuNSllVBDkWdwa4Ahi0VtsUs8bUtkj1gScoiGho8UEFABZCgwjQIDAmcrqTwsAAeIEI5GIgjwEDAkAgZUy4k53PIz35rmhpnUmQARhLCEh-MQQBhipAwQqQABjFWizIYDXdciikAAEwlCD4auItCZzmw8pG0kUTxhajCImsujGQA" width="800" height="800"></iframe>
Reducció de funcions iteratives#
Moltes vegades podem trobar una solució més eficaç a un problema analitzant un problema més senzill.
És el cas dels sumadors. Si volem sumar dos nombres de 8 bits fent la taula de veritat tindríem \(2^{16} = 65536\) combinacions a la taula de veritat. Massa feina!
El que podem fer és analitzar com sumem els bits. Sumem els bits de la mateixa posició, tenint en compte si ens enportem un 1 de la suma de la posició anterior ( a la dreta) i anotem el resultat i, si és el cas, ens enportem un 1 a la suma següent (posició esquerra). Per tant, el nostre problema es simplifica a sumar dos bits amb un possible bit extra (CARRY) de la suma anterior i obtenir el resultat i el nou CARRY.
\(a_i\) |
\(b_i\) |
\(c_{i-1}\) |
\(c_i\) |
\( s_i\) |
|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Ara aplicariem el que hem après i tindríem l’esquema de oportes lògiques per a les dues sortides.
Al simulador veurem una altra solució que utilitza portes XOR:
Show code cell source
%%html
<iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWc0FwCwCY0HYEA4cEMElURTJyBTAWjDACgwE1w1WNsMRPveoeAhExYgAzGIBsPBNLSSOsgd0rCA7jy6buYyBy2QGG3fp1TtUI+PNhJlfrcqHj5rPa1vLG-p59YvFhj+YOw8-s4WjoHhVhh4eOBxIPKsYEmGALLkAJzcUZLBdoIYKFb0fPFsHJURIalpIHiU5QFN4A1txNIRnUp1Mt0MADKN9kpoCV2ClABmAIYANgDOVOSWIy1xCRM8lSog88urSIYboUGsOxfTB4sra7Wh-S39tQ3PDVsBKYnbClUBCTSMC5cR6cCgiImCE6cH8CI-KYIbDSKYRZGopQYniQBKZcgonEJAocXHFUrMZpPJJfNJ4m7CSnWYGEn5gQn2IQibhsooIUFRTmqBhAA" width="800" height="800"></iframe>
Repetint aquest bloc 8 vegades i encadenant-los podem ara resoldre el nostre problema original.
Nosaltres ens conformarem amb repetir-lo 4 vegades i tenir un sumador de dos nombres de 4 bits:
Show code cell source
%%html
<iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcMBMcUHYMGZIA4UA2ATmIxAUgoqoQFMBaMMAKDGMJDTxABYxOKBJ36DwbDl3xc8PIYNldx7QdIFV54QhuWTuIbCi7CDRo6wAyUnofAobRqlQBmAQwA2AZzrVILK5KEvCCStlQQbl4+SH4A7iGcQdYgSXEJ4MRmaplQ-unsRpLqUCWR3r55+sVg9lpO4CBl0blW+vY8NXKK9U0VAZyGVHrdDb0xLPGhaMmDuZMivHLSvIst6Ss8kqIlER7l463LAnY82+GNe81puMHbNwZ4wdeQwdiPM+9p+m-B3wiOEwMLxkNmBmmevxMbRMX2kmjaKCegPuxRRtQhJ2SnTmWNq+kkfgAskDXkZsIQHCUUNAECxifdQhT0hoaXSSVxEQYmShOSzafTgdh-lybMK+Wz7osqOTTnh6tTaQAPEDvPDEcDCnK-YIAI2wAB1PK5sCxlXhyDzzAgkDykNqQDqUIbXChTSqyQh1WBKFyjPadWBnawzdg+IpvRBeMRI1xdZBnX5lbxIBByXxath1fbPLw3ZnNlmhMg-bGQJ4TcrM+qeeReEQuLg+KXPK7K8RRbWi+SqNngwZ22G-UXFnbm35+Fm5WGKLVVrRAVLp5KeBjVvcwsjgaFgVOMVPF7vN79OSichiCqZwmfkdML7NmAD4veamHwi+MUKyYLph-ptg07M1wAX+aZgCsOL-pwYG3FO0EQcCi6SnOR58Ksi4bDii5gBgIj7shE4gAwRScAwqzHGAkCcrm8TfFkK44vo0qOBBzG2McsIdNoWLgRx4DgbBPE3tO+4roCIkquEgk0XCihtBgj7JJgRhJEpLESSkwSHvESRTip8lqQ+06GWkZEvmhcAMUcqinBZvHJj2NlOCwBFEQMTKkTYTIUVRgL6BhfmpL5yxJLYvCBdJDgaNIkGWTYaYhWm1x+rYSS8Bu2m3ClryJUFPAqdIWmmCKRXYklmIXqVgIVbUF6FbVUU8IVVQ5G00i8VUOHJGV9lFT8al9dhAyfFVnUDZ1jEsEAA" width="800" height="800"></iframe>
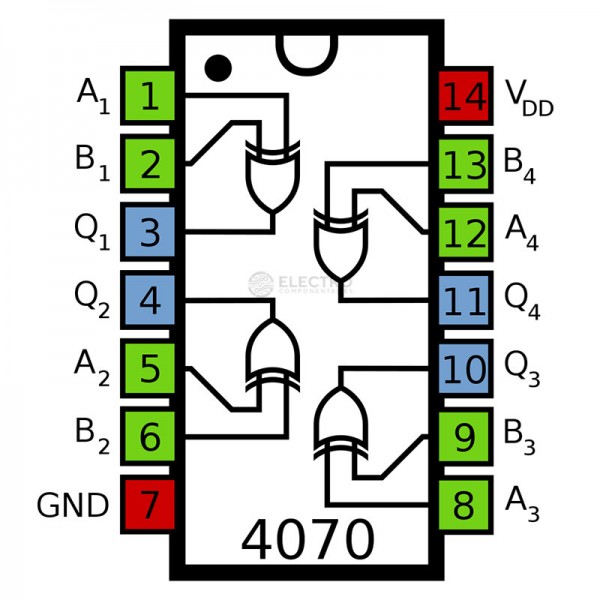
Aquet dispositiu es pot trobar comercialitzat com a 74LS83. El seu pin-out és aquest:
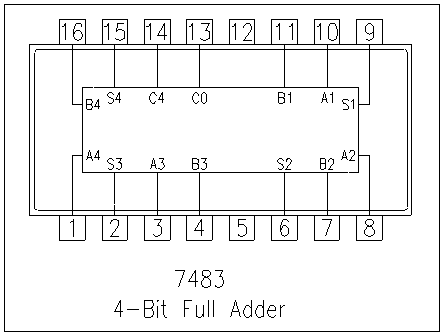
Reducció a portes NAND#
OR |
AND |
NOT |
|---|---|---|
Famílies lògiques#
Una família lògica és una implementació de les portes lògiques amb transistors (algunes també fan servir diodes) amb una tensió d’alimentació i uns nivells lògics compatibles. Veiem uns exemples molt típics:
Tecnologia |
L |
H |
Tensió d’alimentació |
|---|---|---|---|
0 V a 0,8 V |
2 V a V CC |
V CC = 5 V |
|
0 V a 30% V DD |
70% V DD a V DD |
Si bé podríem implementar una porta NAND amb només 2 transistors (com efectivament es fa a la família lògica NMOS), aquesta compatibilitat necèssaria de nivells lògics i tensions d’alimentació obliguen a adaptar els dissenys a cada família. Al simulador podeu veure diverses implementacions a Circuiits -> Logic families
Show code cell source
%%html
<iframe src="https://www.falstad.com/circuit/circuitjs.html?ctz=CQAgjCAMB0l3BWcMBMcUHYMGZIA4UA2ATmIxAQBYKLIKBTAWjDACgAzETFLla7bIV7VqYaEhiQUrAO4gBQsJX6DwGIZFnzVYddqFo8UVgFl9aoZTgWoXcRy4YeKPEYVdXIUeKixpc9z46QKdjAHNzXBUhdzpNOSCQPGDVZOMA1JTFMB5NACUuKyS6XSE0uK86CVsYBC1SjyNuRuMAGUdnPnAc4VsIdgBDABsAZ3oaTXaGlyMWZ08SkEHR8YlWACdzOa3lWwR4ViA" width="800" height="800"></iframe>
A un circuit integrat CMOS una porta NAND té la següent estructura a l’oblea de silici:
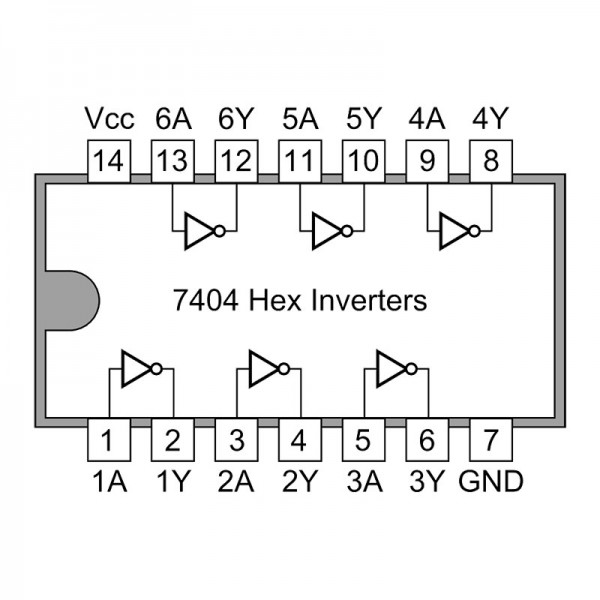
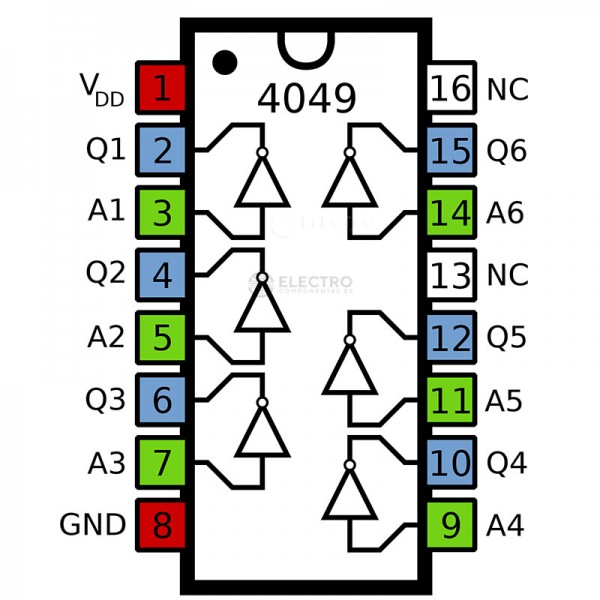
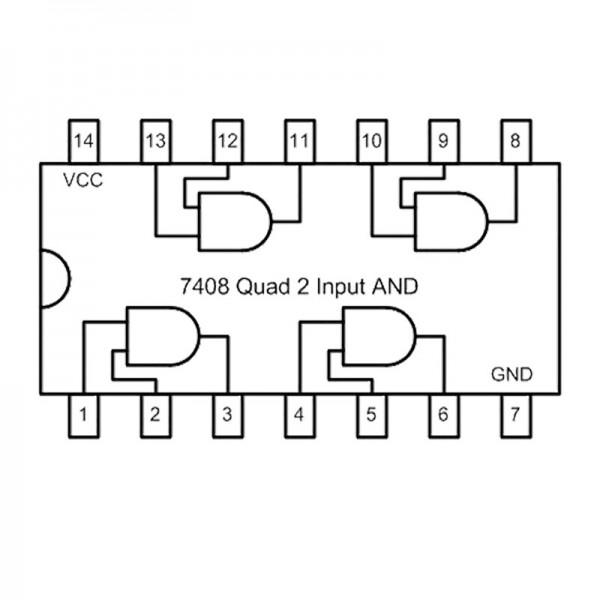
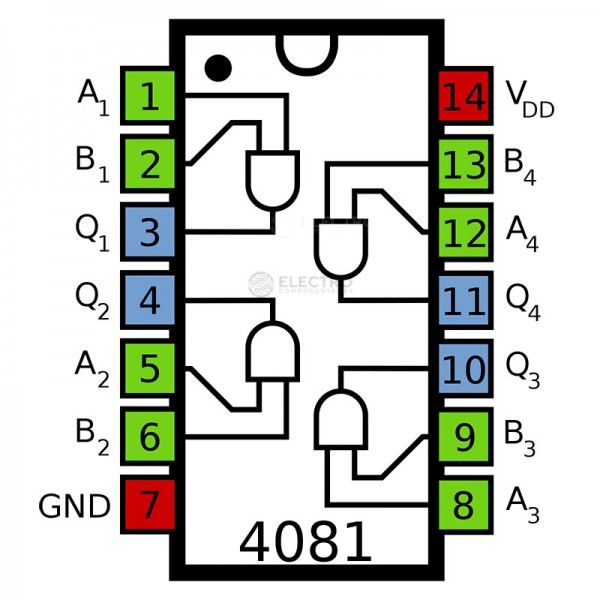
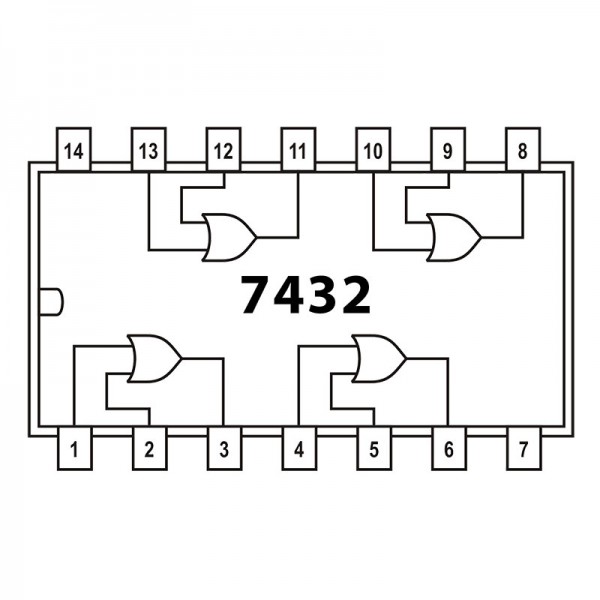
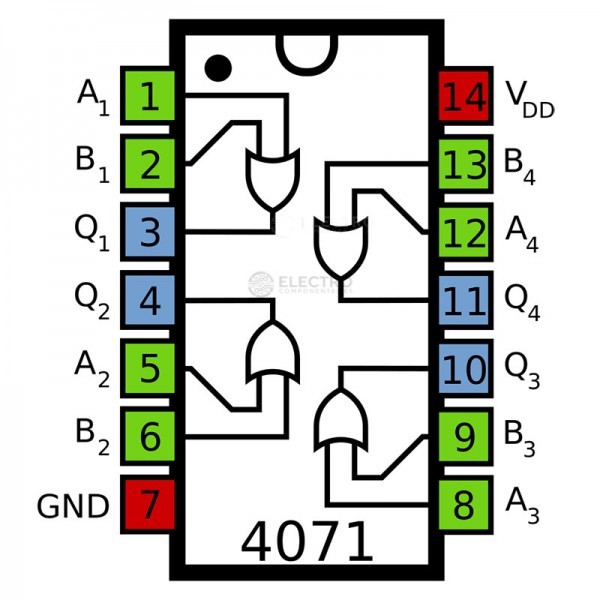
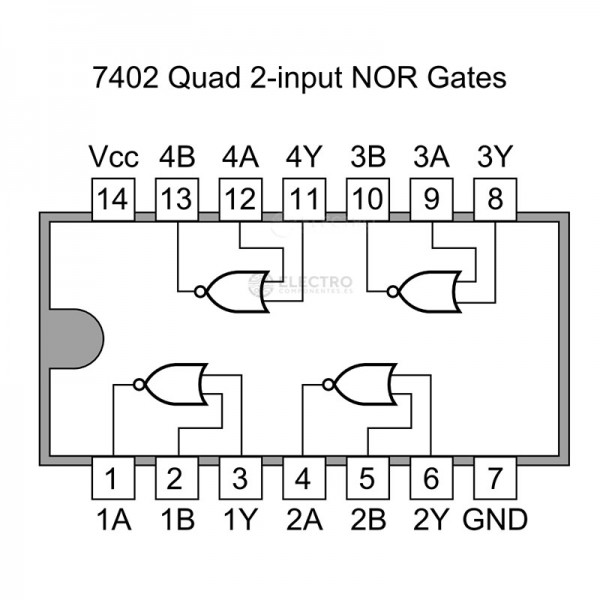
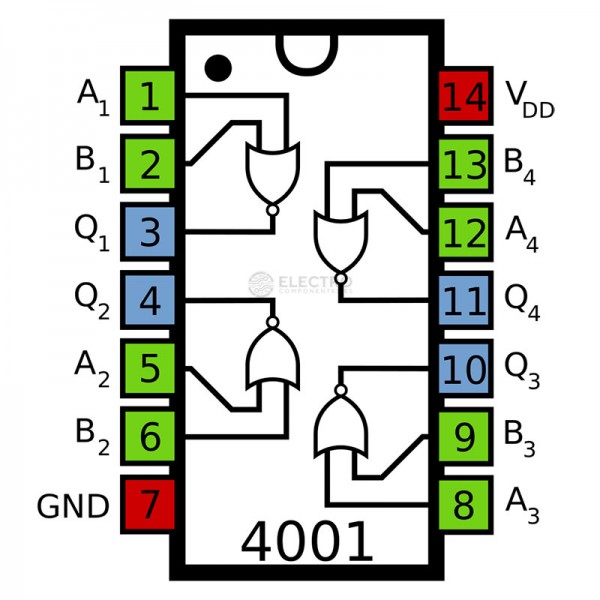
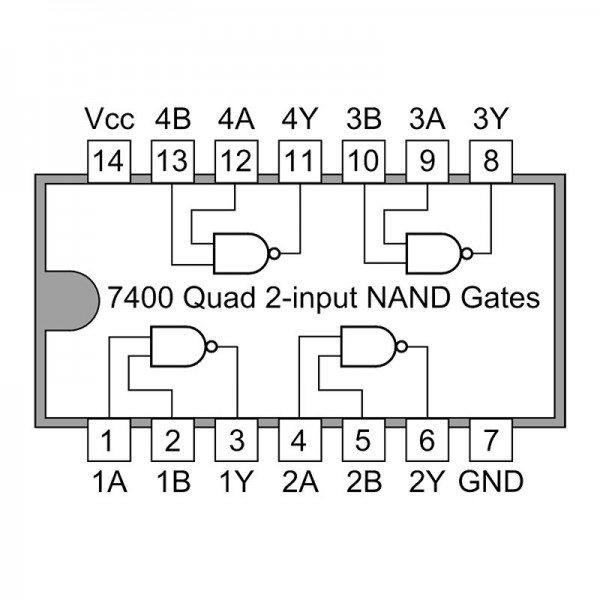
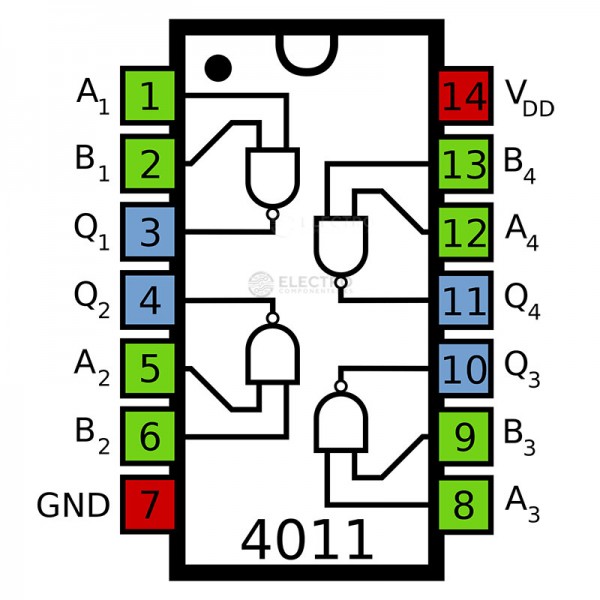
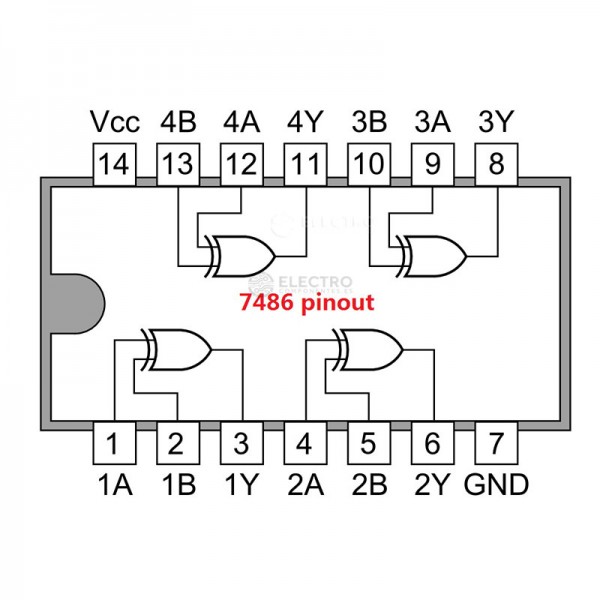
Productes comercials#
Porta lògica |
C.I. TTL |
pin-out |
C.I. CMOS |
pin-out |
|---|---|---|---|---|
NOT |
|
|
||
AND |
|
|
||
OR |
|
|
||
NOR |
|
|
||
NAND |
|
|
||
XOR |
|
|
Dispositius programables: PAL, GAL, FPGA.#
També podem treballar amb dispositius programables que permeten introduir la nostra funció lògica.
Els mé simples són les PAL (Programmable Array Logic) on tens un minterm amb tots els termes possibles i aplicant un voltatge superior al d’alimentació cremes uns fussibles que eliminen els termes no dessitjats de la funció:
Les GAL (Generic Array Logic) van ser un pas endavant: es poden reprogramar i es poden configurar els pins com a entrada o sortida. Malgrat es va considerar un producte obsolet fa uns anys alguns fabricants han tornat a fabricar aquests xips, com és el cas del GAL22V10, donada la seva demanda.
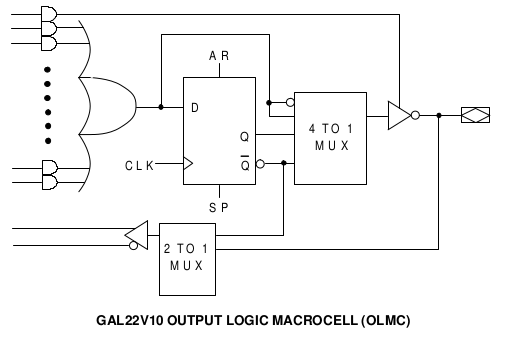
Els més sofisticats són les FPGA (field-programmable gate array), que es poden reprogramar. Avui en dia podem trobar FPGAs amb 50 milions de portes lògiques integrats.
Un exemple utilitzat a la docència i al món maker és el xip iCE40HX4K-TQ144, que porta 3520 elements lògics integrats i que és el cor de la placa Alhambra II, que es pot programar amb l’entorn lliure icestudio i té un factor de forma Arduino UNO. Amb aquest entorn és possible reproduir un microprocessador Z80 o una rèplica de la CPU de l’ordinador de navegació que va aterrar l’Apolo XI a la lluna.