Tractament matemàtic del corrent altern. Nombres complexos. Fasors#
Pàgina en desenvolupament
Encara estem treballant en aquest document.
Esperem oferir-vos properament el seu contingut.
Disculpeu les molèsties.
La solució per tractar matemàticament el corrent AC passa per treballar amb nombre complexos i les seves diferents representacions.
Recordem la representació al pla complex d’un nombre \(z\) i el seu conjugat:
Nosaltres utilitzarem la lletra j per a indicar \(\sqrt{-1}\), ja que la lletra i la utilitzem per a la intensitat instantània.
Forma binòmica#
\(z = a + jb\)
conjugat#
\(\overline{z} \equiv a - jb\)
Forma mòdul-argumental#
\(z = R_{\varphi}\)
Divisió#
\(x = X_{\alpha}\)
\(y = Y_{\beta}\)
\(\frac{x}{y} = \frac{X_{\alpha}}{Y_{\beta}} = Z_{\varphi}\)
on
\(Z = \frac{X}{Y}\)
\(\varphi = \alpha - \beta\)
Forma trigonomètrica#
\(z = Rcos(\varphi) + jRsin(\varphi)\)
Forma exponencial#
\(z = Re^{j\varphi}\)
Fasors#
Ara podem representar la tensió i la intensitat com a nombres complexos, anomenats fasors
receptors |
gràfic |
fasor |
|---|---|---|
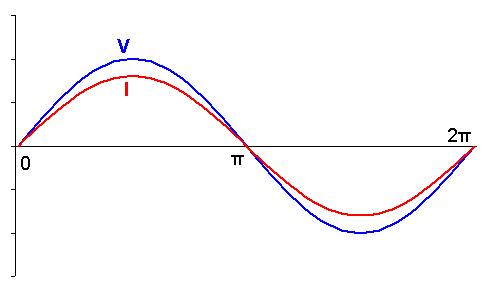
R |
|
|
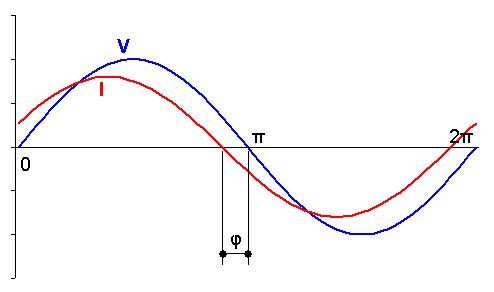
C, R |
|
|
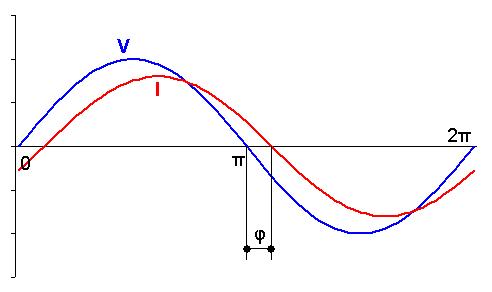
L, R |
|