Xocs inelàstics#
Dos cotxes amb massa m= 1000 kg circulen a 60 km/h i xoquen frontalment, quedant aturats. Calculeu
a) L’energia alliberada en forma de calor per a cada cotxe.
b) Els temps de frenada si els frens a cada cotxe exerceixen una força constant F = 4 kN
c) L’espai recorregut en aquesta frenada
d) Repetiu els apartats anteriors si la velocitat fos el doble (120 km/h)
Solució#
Veiem que podem fer amb el que sabem de teoria.
A l’apartat (a) es tracta d’un xoc inelàstic amb velocitat final = 0 m/s on tota l’energia cinètica es dissipa en forma de calor:
\(Q = \Delta E = Ec(v=v0)\)
\(Ec = \frac{1}{2} \cdot m \cdot v^{2}\)
A l’apartat (b) tenim un M.U.A. amb acceleració negativa que acaba al repòs:
\(F = m \cdot a \Rightarrow a = \frac{F}{m}\)
\(v = v_{0} + a \cdot t\)
\(\Delta r = v_{0} \cdot t + \frac{1}{2}\cdot a \cdot t^{2}\)
Per tant, sembla que introduïnt les dades a les fòrmules tenim resolt el nostre problema
Anem a la pràctica …
Treballant amb unitats a python. La llibreria pint#
La llibreria pint ens permet treballar amb unitats, fer conversions i donar més rigor als càlculs
Teniu un bon tutorial a https://pint.readthedocs.io/en/0.13/tutorial.html
from pint import UnitRegistry
ureg = UnitRegistry()
m = 1000 * ureg.kg
v0 = 60 * ureg.km / ureg.hour
El primer pas seria tenir les dades en Sistema Internacional. Fixeu-vos que la llibreria pint s’encarrega d’això.
Si bé v0 el tenim en \(\frac{km}{h}\)
v0
Sempre podem convertir una dada al Sistema Internacional amb .ito_base_units()
v0.ito_base_units()
v0
Podem millorar l’expressió gestionan el format de sortida:
'Velocitat inicial en S.I: {:P~}'.format(v0)
'Velocitat inicial en S.I: 16.666666666666668 m/s'
Si haguessim fet nosaltres mateixos la conversió obtindriam el mateix valor:
v0 = 60 * ureg.km / ureg.hour
v0 = v0 * 1000 * ureg.m / ureg.km * ureg.hour / (3600 * ureg.s)
v0
Encara que de vegades haurem de forçar la simplificació d’uniotats amb ito_reduced_units() (veure https://pint.readthedocs.io/en/0.13/tutorial.html#converting-quantities)
density = 1.4 * ureg.gram / ureg.cm**3
volume = 10*ureg.cc
mass = density*volume
print(mass)
14.0 cubic_centimeter * gram / centimeter ** 3
mass.ito_reduced_units()
mass
Ara que sabem com treballar amb unitats a python ens podrem dedicar a resoldre el nostre problema
a) L’energia alliberada en forma de calor per a cada cotxe.#
Ara ja podem calcular la energia cinética de cada cotxe \(Ec=\frac{1}{2}\cdot m\cdot v^{2}\)
Ec=1/2*m*v0**2
Ec
Naturalment l’energia es mesura en J. Podem fer el canvi amb .ito(ureg.J)
Ec.ito(ureg.J)
Ec
I tenir-la amb un múltiple adient. pint ho pot fer amb .to_compact
print (Ec.to_compact())
138.8888888888889 kilojoule
Que justament és alliberada en forma de calor per a cada cotxe
L’expresió correcta d’aquest resultat seria Q = 138,8 kJ
b) Els temps de frenada si els frens a cada cotxe exerceixen una força constant F = 4 kN#
Com la força de frenada s’oposa a la velocitat tindrà signe negatiu:
F = -4 * ureg.kN
a = F / m
a
Ho arreglem amb .ito_base_units()
a.ito_base_units()
a
t = (0 * ureg.m / ureg.s - v0) / a
t
Per tant tindrem un tems de frenada t = 4,167 s
c) L’espai recorregut en aquesta frenada#
r = v0 * t + 1 / 2 * a *t**2
r
Es a dir, l’espai recorregut en aquesta frenada derà de r = 34,72 m
d) Repetiu els apartats anteriors si la velocitat fos el doble (120 km/h)#
Podem repetir les fòrmules, canviant el valor inicial de v0:
v0 = 120 * ureg.km / ureg.hour
v0.ito_base_units()
v0
Ec=1/2*m*v0**2
Ec.ito(ureg.J)
print (Ec.to_compact())
555.5555555555557 kilojoule
a) Q” = 555,6 kJ
t = (0 * ureg.m / ureg.s - v0) / a
t
b) t” = 8,333 s
r = v0 * t + 1 / 2 * a *t**2
r
c) r = 138,9 m
Conclusions#
Comparem resultats:
| v0 | Q | t | r |
| 60 km/h | 138,8 kJ | 4,167 s | 34,72 m |
| 120 km/h | 555,8 kJ | 8,333 s | 138,9 m |
Si bé el temps s’ha duplicat com la velocitat inicial, la calor dissipada i la distància recorreguda s’han multiplicat per 4. Això és degut a la depèndencia quadràtica de Q i r amb la velocitat inicial. El temps t, en canvi, té una dependència linial amb v0
Veiem gràficament aquestes dependències:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('bmh')
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 50, 1000)
ax.plot(x, 1 / 2 * x * x);
plt.title("Calor dissipada a cada cotxe")
plt.xlabel("v [m/s]")
plt.ylabel("Q [kJ]");
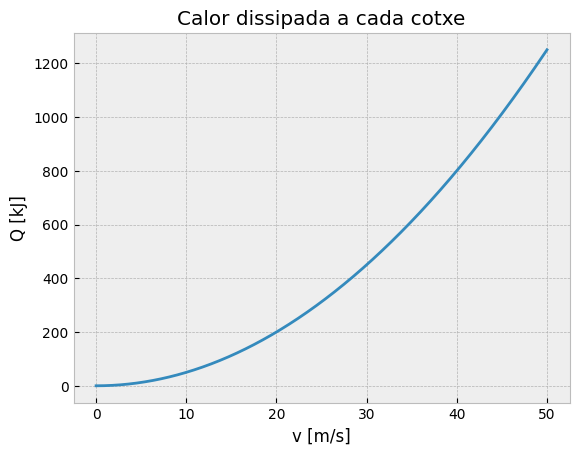
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 50, 1000)
ax.plot(x, x / 4);
plt.title("Temps de frenada")
plt.xlabel("v [m/s]")
plt.ylabel("t [s]");
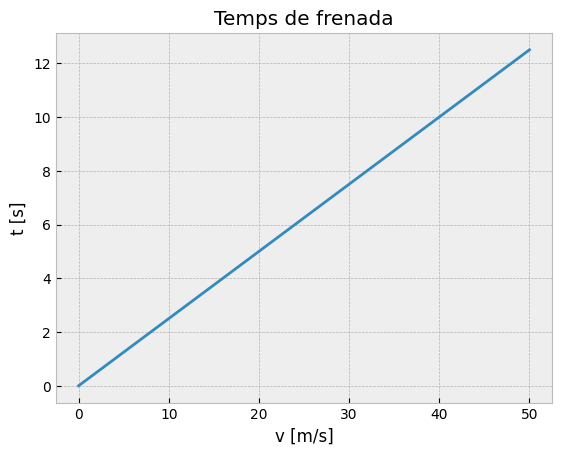
Com imagineu, la gràfica de l’espai recorregut a la frenada és més difícil de fer, ja que depén de v0 i de t, que també depèn de v0. Però no per això aquesta dependència quadràtica és menys important, com sabreu tots els que estudieu per treure’s el carnet de conduir!
\(v = v_{0} + a \cdot t = 0 \Rightarrow t = - \frac{v_{0}}{a} \)
\(\Delta r = v_{0} \cdot t + \frac{1}{2}\cdot a \cdot t^{2}\)
\(\Delta r = v_{0} \cdot (- \frac{v_{0}}{a}) + \frac{1}{2}\cdot a \cdot {(- \frac{v_{0}}{a})^{2}}\)
\(\Delta r = - \frac{(v_{0})^{2}}{a} + \frac{1}{2}\cdot \frac{(v_{0})^{2}}{a} = \frac{1}{2} \frac{(v_{0})^{2}}{a}\)
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 50, 1000)
ax.plot(x, 1 / 2 * x * x / 4);
plt.title("Recorregut de frenada")
plt.xlabel("v [m/s]")
plt.ylabel("r [m]");
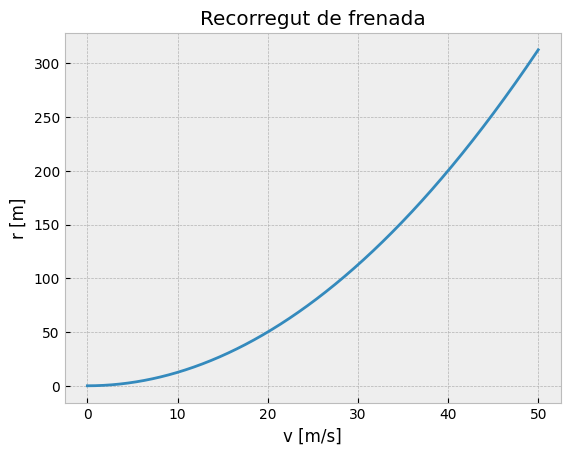
Representem la mateixa corba posant la velocitat en \(\frac{km}{h}\)
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 50, 1000)
ax.plot(x * 3.6, 1 / 2 * x * x / 4);
plt.title("Recorregut de frenada")
plt.xlabel("v [km/h]")
plt.ylabel("r [m]");
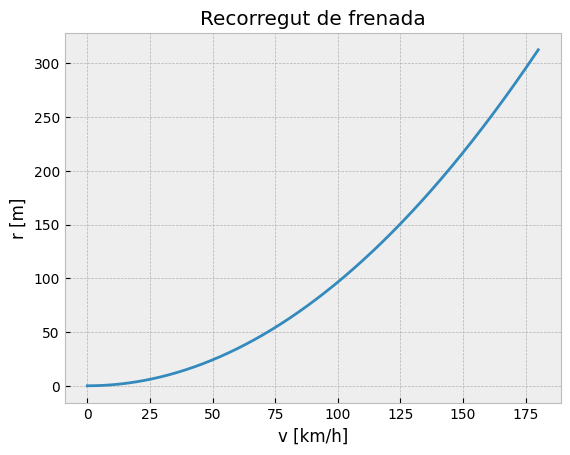
Com veieu per a una acceleració de - 4 \(\frac{m}{s}\) es compleix la regla de dividir per 10 i elevar al quadrat la velocitat en \(\frac{km}{h}\) per obtenir la distància de seguretat en \(m\). Aquesta acceleració correspon a 0,4g , valor raonable en un cas real.